Exponentialfunktion
Alles um uns herum wächst oder vermehrt sich bzw. stirbt. Daher ist es ganz natürlich sich damit auseinander zu setzen und zu versuchen diese Vorgänge in Formeln zu fassen und so handhabbarer zu machen. Als Einstieg in diese ausgesprochen spannendes und vielseitiges Thema kann der Versuch des Bierschaumzerfalls dienen.
Experiment: Bierschaumzerfall
Aufgabe
In ein möglichst zylinderförmiges Glas wird Bier (am Besten Malzbier) eingeschenkt. In der folgenden Messung wird die
Höhe des Bierschaums gemessen und gegen die vergangenen Zeit aufgezeichnet.
Lösung
Es ergibt sich folgende Messtabelle:
| Zeit in Min | Höhe in cm | ||
| Unten | Oben | Differenz | |
| 0 | 20 | 3 | 17 |
| 1 | 19 | 7 | 12 |
| 2 | 18 | 8 | 10 |
| 3 | 17 | 9 | 8 |
| 4 | 16 | 9 | 7 |
| 5 | 15,5 | 9,5 | 6 |
| 6 | 15 | 9,5 | 5,5 |
| 7 | 14 | 9,5 | 4,5 |
| 8 | 13 | 9,5 | 3,5 |
| 9 | 12,5 | 9,5 | 3 |
| 10 | 12 | 9,5 | 2,5 |
| 11 | 11,5 | 9,7 | 1,8 |
| 12 | 11 | 9,7 | 1,3 |
| 13 | 10,5 | 9,7 | 0,8 |
Aufgetragen in einem t-h(t) ergibt sich folgendes Bild:
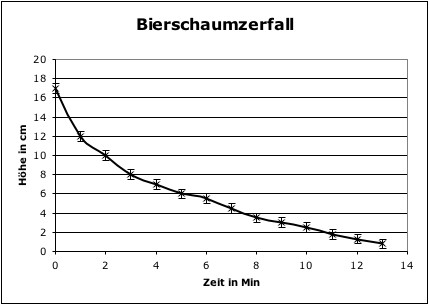
Dieser Versuch sollte durchaus mit anderen Malzbieren und Gläsern durchgeführt werden, um eine Vergleichsmöglichkeit zu bekommen und in ein Gespräch zu kommen: "Welches Schaum ist fester?", "Welche Messgröße beschreibt den Schaum am Besten und Einfachsten?" Dabei sollte herauskommen, dass die Halbwertszeit, eine gute Charakterisierung bildet, da sie einfach zu bestimmen ist und bei unetrschiedlichen schäumen gut differiert.
Definition: Exponentielle Abnahme
f(t) = a · bt/tH
Interpretationen
- a: Startwert
- b = 0,5. In Zusammenhang mit Halbwertszeiten ist dieser Wert immer 0,5.
- tH: Halbwertszeit; die Zeit, nach der nur noch b/2 vorhanden ist
- t: hier die abgelaufenen Zeit
- f(t): Funktionswert zum Zeitpunkt t
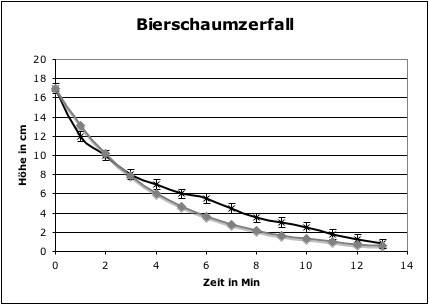
Bei obigem Beispiel lässt sich als Startwert aus der Tabelle 17cm ablesen. Die Halbwertszeit tH bis nur noch 17cm:2=8,5cm vorhanden sind, beläuft sich auf ungefähr 2,7 Minuten ≈ 160s (lässt sich der Grafik entnehmen). Damit lautet die zugehörige Funktionsgleichung:
Analog zur Verringerung der Ausgangsgröße ist auch die Zunahme von Interesse. Hier soll als Beispiel das Bakterienwachstum dienen. Zu
Beginn braucht man wenigstens 1 Bakterium. Nach einer bestimmten Zeitspanne verdoppelt sich die Anzahl der Bakterium auf Grund der
Zellteilung. Man erhält somit folgende Tabelle:
| Zeit in Min | Bakterienanzahl |
| 0 | 1 |
| 1 | 2 |
| 2 | 4 |
| 3 | 8 |
| 4 | 16 |
| 5 | 32 |
| 6 | 64 |
| 7 | 128 |
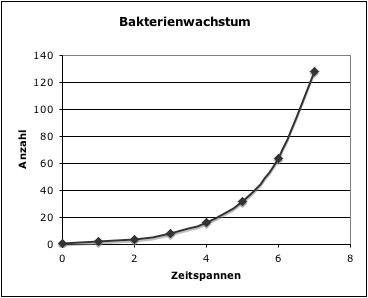
Definition: Exponential-Funktion
f(x) = a · bx
Interpretationen
- a: Startwert
- b: Zuwachsrate (100% + Rate in %)
- x: hier die abgelaufenen Zeit
- f(x): Funktionswert zum Zeitpunkt t
Beispielaufgabe
Aufgabe
In einer Baktierienkultur werden nach 2 Stunden ca. 800 und nach 8 Stunden 30000 Bakterien bestimmt. Wie viele Bakterien waren nach 3 Stunden vorhanden?
Lösung
Zunächst muss die Funktionsgleichung f(x) = a · bx bestimmt werden. Leider ist weder a noch b direkt angegeben. Da aber 2 Funktionswerte gegeben wurden f(2)=800 und f(8)=30000 lässt sich der Term dennoch exakt bestimmen. Denn eine Gleichung lässt sich immer genau dann exakt bestimmten, wenn die Anzahl der unbekannten Paramter gleich der Anzahl der gegebenen Wertpaare ist.
Man erhält somit zunächst folgende beiden Gleichungen:
30000 = a·b8
Löst man die beispielsweise die zweite Gleichung nach a auf (a=30000·b-8), so lässt sich das a in der ersten Gleichung
ersetzen:
800 = 30000·b-6 |·b6
800·b6 = 30000 | : 800
b6 = 37,5
|b| = 37,51/6
=> b≈1,83
Der Wachstumsfaktor beträgt somit 183%. Damit lassen sich die beiden Ausgangsgleichungen vereinfachen und man kann z.B. die erste Gleichung nach a auflösen:
a = 800:1,832 ≈ 240.
Die Funktionsgleichung lautet somit f(x) = 240 · 1,83x und nach 3 Stunde ergeben sich f(3) = 240 · 1,833 ≈ 1470.
Beispielaufgabe
Aufgabe
Ruanda hatte hatte 1986 ca. 6 Millionen Einwohner. Wie viele Einwohner wird es 2000 geben, wenn die jährliche Zunahme 3,7 Prozent beträgt?
Lösung
Wieder muss die Funktionsgleichung f(x) = a · bx bestimmt werden. Der Ausgangswert a beträgt 6·106. Die Zuwachsrate beträgt 100%+3,7% = 1,037, da nach einem Jahr mehr Einwohner vorhanden sind. Damit lautet die Funktionsgleichung
Jetzt muss nur noch x,also die Anzahl der vergangenen Jahre eingesetzt werden: 2000-1986=14. Und es ergibt sich
Leider erlebt und erlebte Ruanda sehr viel Elend, so dass diese Vorausssage nicht zutraf.