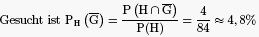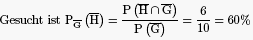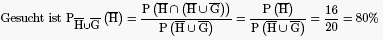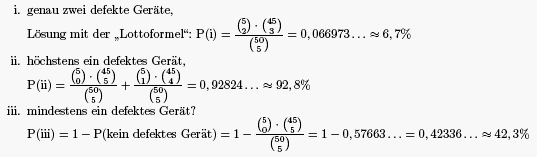Einführung
Die Binomialverteilung ist eine der wichtigsten Verteilungsfunktionen und kommt daher schwerpunktmäßig in der Schule vor. Im Grundkurs ist es meist die einzige die ausführliche behandelt wird. Daher beschränke ich mich hier auch auf diese Funktion.
Eng verbunden mit dem Begriff Binomialverteilung ist der Begriff der Bernoulli-Kette.
Bernoulli-Kette
Damit ein Zufallsexperiment durch eine Bernoulli-Kette modelliert werden kann, müssen zwei Eigenschaften gelten:
- Es interessiert nur ob ein Ergebnis eintrifft oder nicht, also Treffer/Gewinn oder Niete.
- Die Wahrscheinlichkeit für das Eintreten eines Treffers bleibt im Laufe des Experiments gleich.
Gerade die zweite Eigenschaft ist hier wichtig und wird dennoch immer wieder nur angenähert.
Beispiel 1
Aus einer Sendung bestehend aus 200 Glühbirnen sollen 10 Glühbirnen genommen und untersucht werden, ob sie brennen (Treffer) oder nicht (Niete).
Obwohl die Wahrscheinlichkeit für die erste Glühbirne 1/200, für die zweite 1/199, etc beträgt, kann man dennoch das Experiment als Bernoulli-Kette modellieren, da sich die Wahrscheinlichkeiten kaum voneinander unterscheiden.
Ab welcher Menge man eine Bernoulli-Kette zur Modellierung nehmen kann ist schwierig zu sagen und hängt auch von dem Gesamtexperiment ab. Als Faustregel für die Schule kann man folgendes sagen: Entweder steht bereits in der Aufgabestellung, dass die Bernoulli-Kette genommen werden soll oder es sind zu Anfang des Experiments mindestens 100 Dinge vorhanden.
Wie wird nun konkret die Wahrscheinlichkeit für das Auftreten in einem solchem Fall berechnet? Ich konkretisiere das obige Beispiel dadurch, dass die Herstellerfirma der Glühbirnen angibt, dass nur 5 Prozent Ausschuss entsteht. Wie wahrscheinlich ist es nun, dass man genau 4 kaputte Glühbirnen bekommt, wenn man insgesamt 10 zieht?
Anhand einen Baumdiagramms, das leider sehr unübersichtlich zu zeichnen wäre, kann man sich folgendes überlegen:
Eine Möglichkeit wäre es, zunächst 4 mal eine kaputte Glühbirnen zu ziehen (P = 0,054) und anschließend 6 ganze (P = 0,956). Jetzt muss man noch berücksichtigen, dass es ja noch andere Reihenfolgen gibt in denen das gewünschte Ereignis auftritt: 4 aus 10 müssen kaputt sein.
Die Gesamtwahrscheinlichkeit beträgt somit: P(X=4) = (10 über 4) * 0,054 * 0,956 = 0,00096. Die Wahrscheinlichkeit beträgt also ungefähr 0,1 Prozent.
Durch eine Verallgemeinerung dieser Überlegung kommt man zu folgender Formel:
Binomial-Verteilung
Die Wahrscheinlichkeit für das k-fache Aufreten des Ereignisses bei n Versuchen:
![]()
p ist dabei die Aufretenswahrscheinlichkeit für das gewünschte Ergebnis, (1-p) für das Gegenereignis.
Interessiert einen nicht eine "exaktes" Auftreten wie oben, sondern etwas wie "maximal 4 kaputte Glühbirnen", so muss man die gewünschten Wahrscheindlichkeiten für X=0,X=1,X=2,X=3 und X=4 aufsummieren, denn man muss 5 unterschiedliche Bäume betrachten.
Im Beispiel berechnet man somit F(10,0.05,4) = 99,99%. Das bedeutet, dass es so gut wie ausgeschlossen ist (99,99%), bis zu 4 kaputte Glühbirnen unter 10 gezogenen zu haben. Allein die Wahrscheinlichkeit maximal 1 (also 0 oder 1) Kaputte zu bekommen, ist mit ungefähr 60% unwahrscheinlich.
Kumulierte Binomial-Verteilung
Die Wahrscheinlichkeit für das maximal k-fache Aufreten des Ereignisses bei n Versuchen:
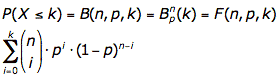
p ist dabei die Aufretenswahrscheinlichkeit für das gewünschte Ergebnis, (1-p) für das Gegenereignis.
Da die Bezeichnung variieren, habe ich alle Schreibweisen angegeben.
Typisch auftretende Wert können in Tabellen nachgeschlagen werden oder durch den angegebenen Rechner berechnet werden.
Rechner
Binomial-Verteilung
Kumulierte Binomial-Verteilung
Signifikanztest
Bleiben wir bei obigem Beispiel. Angenommen, sie machen eine Stichprobe von 10 Glühbirnen und haben 2 kaputte dabei. Stimmt jetzt die Aussage der Firma, dass die Aussschusswahrscheinlichkeit p=0,05 beträgt, oder stimmt sie nicht? Diese Art der Fragestellung nennt man Signifikanttest. Warum signifikant? Ganz einfach, weil die Frage auch so formuliert werden kann: Bei p=0,05 darf exakt eine halbe Glühbirne eine kaputt sein. Um wieviel darf man von dieser Halben abweichen, so dass die Abweichung signifikant ("bemerkbar") ist. Ist eine ganze Glühbirne schon eine signifikante Abweichung?
Eine deutliche bzw. signifikante Abweichung läge bei einer Abweichung von 5% vor. Bei manchen Test ist dies zu grob und man formuliert Hochsignifikanztests mit 2% oder sogar nur einem Prozent. Diese Prozentzahl nennt man dann auch das Signifikanzniveau des Tests und schreibt α=5%.
Um den Test korrekt zu modellieren sollte man sich zunächst überlegen, in welchem Bereich die Anzahl der gezogenen, kaputten Glühbirnen liegen muss, um sagen zu können, dass die Firma falsch lag. Sind zu wenig kaputt ist es nicht schlimm. Sind aber zu viele kaputt, so stimmt die Aussage der Firma nicht. Man könnte aus dem Stegreif also schätzen: "Wenn mehr als eine Glühbirne kaputt ist, also {2,3,....10}, so stimmt die Aussage der Firma nicht." Die Behauptung der Firma bzw. die Hypothese ist falsch und wird abgelehnt. Die Menge A = {2,3,....10} nennt man Ablehnungsbereich. Dementsprechend wäre A = {0,1} der Annahmebereich. Da der Ablehnungsbereich rechts von 1 liegt spricht man von einem rechtsseitigen Test. Entsprechend gibt es auch linksseitige und beidseitige Tests.
Leiten wir nun die Formel zur Berechnung her:
α ≥ P("mehr als 1 kaputte Glühbirne in der Stichprobe")
= P("2 oder 3 oder ... oder 10")
= 1 - P("0 oder 1")
= 1 - [P(0) + P(1)]
= 1 - F(n,p,1)
Gesucht ist eigentlich die 1 in F(n,p,1), also die Frage: Ab welchem Anzahl an kaputten Birnen ist die Hypothese der Firma falsch und kann abgelehnt werden. Man stellt 1-F(n,p,C)≤α auf und bestimmt mit Hilfe passender Tabellen die Zahl C.
Für eine linksseitigen Test sieht das Verfahren ähnlich aus:
α ≥ P("weniger als 2 kaputte Glühbirne in der Stichprobe")
= P("0 oder 1)
= P("0 oder 1")
= P(0) + P(1)
= F(n,p,1)
Bei einem beidseitigen Test müssten dann beide Fälle untersucht werden.
Hypothesentest
- Nullhypothese H0: Jemand stellt die Hypothese auf, dass p einen bestimmten Wert hat.
- Der Stichprobenumfang ist n
- Das Signifikanzniveau α = 5%
Linksseitiger Test
![]()
Rechtsseitiger Test
![]()
Beidseitiger Test
![]() und
und ![]()
Binomial-Verteilung
Aufgabe 1
Eine Firma stellt Heizlüfter her. Bei der Endkontrolle wird die Funktion des Gebläses und die Funktion des Heizelements überprüft. Dabei stellt sich heraus, dass bei 90 % der Geräte das Gebläse in Ordnung ist. Bei insgesamt 16 % der Lüfter ist das Heizelement defekt. Bei 37,5 % der Geräte mit defektem Heizelement ist zusätzlich das Gebläse nicht in Ordnung.
a) Wie viel Prozent der Geräte sind in der Endkontrolle einwandfrei?
Lösung von Aufgabe 1a)
b) Mit welcher Wahrscheinlichkeit hat ein Gerät mit funktionierender Heizung ein defektes Gebläse?
Lösung von Aufgabe 1b)
c) Mit welcher Wahrscheinlichkeit ist bei einem Gerät mit defektem Gebläse zusätzlich das Heizelement nicht in Ordnung?
Lösung von Aufgabe 1c)
d) Mit welcher Wahrscheinlichkeit ist bei einem Gerät, das in der Endkontrolle aussortiert wurde, das Heizelement defekt?
Lösung von Aufgabe 1d)
e) Untersuche den Ausfall des Gebläses bzw. des Heizelementes auf stochastische Abhängigkeit.
Lösung von Aufgabe 1e)
f) Aus Versehen sind unter eine Lieferung von 50 Heizlüftern an einen Großhändler auch 5 defekte Geräte geraten. Ein Einzelhändler ordert 5 Geräte. Mit welcher Wahrscheinlichkeit erhält er darunter genau zwei defekte Geräte, höchtens ein defektes Gerät bzw. mindestens ein defektes Gerät?
Lösung von Aufgabe 1f)
g) Nach einer Änderung bei der Produktion der Gebläse soll untersucht werden, ob sich diese auf die Ausschussquote bei diesem Bauteil ausgewirkt hat. Der laufenden Produktion soll dazu eine Stichprobe von 50 Geräten entnommen und untersucht werden. Bei welchen Ergebnissen dieser Stichprobe wird man (bei einer Irrtumswahrscheinlichkeit von 7,5%) von einer Änderung der Ausschussquote ausgehen?